homeprojectswriting
A graphical interpretation of sinusoidal positional encodings
February 21, 2025

In the original transformer architecture, Vaswani et al. introduced sinusoidal positional encodings, given by

PE(pos,2i)=sin⁡(pos/100002i/dmodel)\mathrm{PE}_{(\mathrm{pos}, 2i)} = \sin(\mathrm{pos}/10000^{2i/d_{\mathrm{model}}}) PE(pos,2i+1)=cos⁡(pos/100002i/dmodel)\mathrm{PE}_{(\mathrm{pos}, 2i + 1)} = \cos(\mathrm{pos}/10000^{2i/d_{\mathrm{model}}})

In their words:

We chose [sinusoidal encoding] because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset kk, PEpos+k\mathrm{PE}_{\mathrm{pos} + k} can be represented as a linear function of PEpos\mathrm{PE}_{\mathrm{pos}}. (Vaswani et al.)

To see the linearity, first write (by the trigonometric angle sum identities)

PE(pos+k,2i)=sin⁡((pos+k)/100002i/dmodel)=PE(pos,2i)PE(k,2i+1)+PE(k,2i)PE(pos,2i+1)\begin{aligned} \mathrm{PE}_{(\mathrm{pos} + k, 2i)}\\ = \sin((\mathrm{pos} + k)/10000^{2i/d_{\mathrm{model}}})\\ = \mathrm{PE}_{(\mathrm{pos}, 2i)}\mathrm{PE}_{(k, 2i + 1)} + \mathrm{PE}_{(k, 2i)}\mathrm{PE}_{(\mathrm{pos}, 2i + 1)} \end{aligned}

for the even dimensions and

PE(pos+k,2i+1)=cos⁡((pos+k)/100002i/dmodel)=PE(pos,2i+1)PE(k,2i+1)−PE(k,2i)PE(pos,2i)\begin{aligned} \mathrm{PE}_{(\mathrm{pos} + k, 2i + 1)}\\ = \cos((\mathrm{pos} + k)/10000^{2i/d_{\mathrm{model}}})\\ = \mathrm{PE}_{(\mathrm{pos}, 2i + 1)}\mathrm{PE}_{(k, 2i + 1)} - \mathrm{PE}_{(k, 2i)}\mathrm{PE}_{(\mathrm{pos}, 2i)} \end{aligned}

for the odd ones. Now note that

PEpos+k≔[PE(pos+k,2i)PE(pos+k,2i+1)]\mathrm{PE}_{\mathrm{pos} + k} \coloneqq \begin{bmatrix} \mathrm{PE}_{(\mathrm{pos} + k, 2i)}\\ \mathrm{PE}_{(\mathrm{pos} + k, 2i + 1)} \end{bmatrix} =[PE(k,2i+1)PE(k,2i)−PE(k,2i)PE(k,2i+1)][PE(pos,2i)PE(pos,2i+1)],=\begin{bmatrix} \mathrm{PE}_{(k, 2i + 1)} & \mathrm{PE}_{(k, 2i)}\\ -\mathrm{PE}_{(k, 2i)} & \mathrm{PE}_{(k, 2i + 1)} \end{bmatrix} \begin{bmatrix} \mathrm{PE}_{(\mathrm{pos}, 2i)}\\ \mathrm{PE}_{(\mathrm{pos}, 2i + 1)} \end{bmatrix},

which is a rotation of PEpos\mathrm{PE}_{\mathrm{pos}}.

However, I prefer to emphasize the fact that sinusoidal encodings capture both long-range and short-range dependencies. Consider the following heatmap, which plots PE\mathrm{PE} (color) against dimension and sequence position:

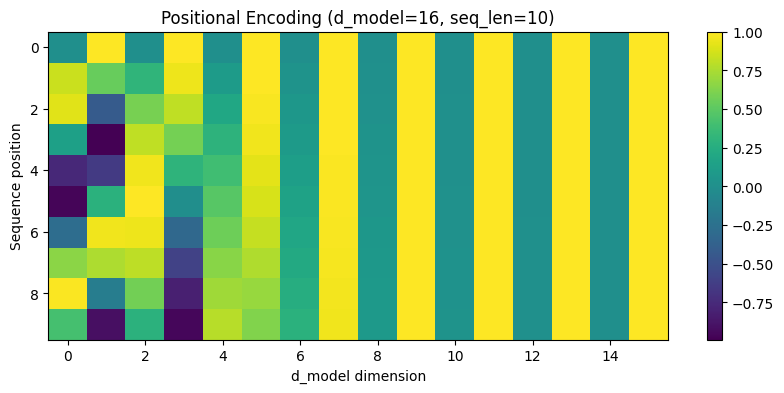
heatmap_10

For small ii, the period of the sinusoidal functions is minimized, leading to greater variation among nearby tokens. Note that in the leftmost column, highly variable colors cluster together.

But a small period makes it harder to distinguish between distant positions. Say we increase the sequence length to 50:

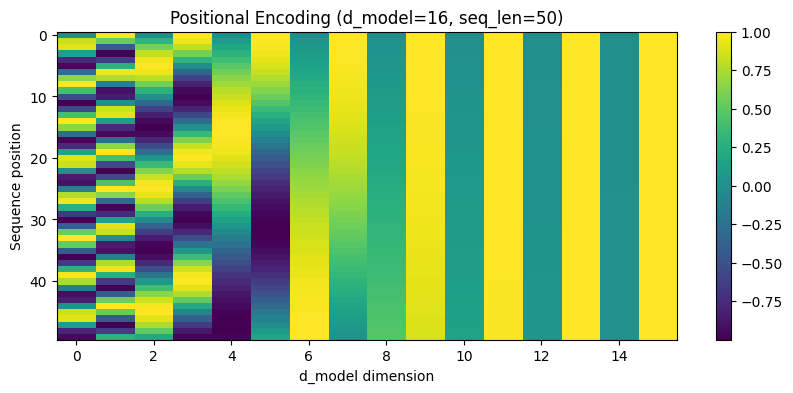
heatmap_50

While dimension 0 assigns identical values to positions 0 and 41, among others, dimensions 4-7 (which have lower frequency) clearly differentiate between them.